Curves and Transformations
Curves
So far we have been working with straight lines, but MetaPost is also great at drawing smooth curved paths.
If you recall from the chapter on variables a path is simply a combination of pairs and connections between them.
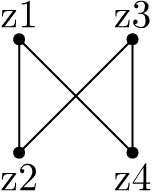
To connect them with a curved path we use .. rather than the -- we have been using so far for straight lines, we can mix .. and -- as we please.
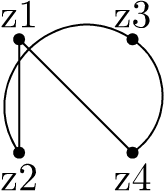
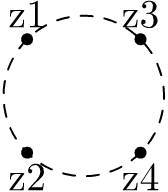
beginfig(3);
z1=-z4=(-1u,1u);
z3=-z2=(1u,1u);
dotlabel.top("z1",z1);
dotlabel.bot("z2",z2);
dotlabel.top("z3",z3);
dotlabel.bot("z4",z4);
draw z1..z2..z4..z3..cycle dashed evenly;
endfig;Transformations
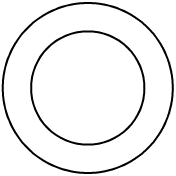
We just saw one way of drawing a circle in MetaPost, we can also use the build in variable fullcircle.
Lets draw a two circles next to each other:
draw fullcircle;
draw fullcircle shifted (1cm,0);

shifted is an example of a transform, it simply adds a pair to every pair in the transformed path.
Other commonly used transforms are rotated and scaled and xscaled,=yscaled=.
rotated rotates pairs around the origin a given number of degrees counter-clockwise
z1 = (1,1);
z2 = z1 rotated 90;
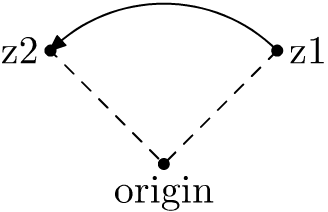
Scaled simply multiplies the x, y or both coordinate with a given factor
u:=1cm;
draw fullcircle scaled u;
draw fullcircle scaled 1.5u;
Combining transforms
We can construct new transformations by combining existing combinations into a Transform variable.
To start off use the special identity transform which does nothing on it's own.
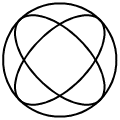
beginfig(4);
u:=1cm;
transform T;
T = identity xscaled -1u yscaled 0.5u rotated 45;
draw fullcircle scaled u;
draw fullcircle transformed T;
draw fullcircle transformed T rotated 90;
endfig;Exercises
You can specify the direction a path enters and leaves a point at, by putting a direction keyword (left,right,up,down)
in curly braces before or after the point in the path definition. You can also specify a custom direction using dir x
where x is a an angle in degrees (moving counter clockwise with dir 0 being straight to the right).
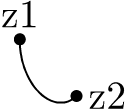
beginfig(1);
z1=(0,1u);
z2=(1u,0);
dotlabel.top("z1",z1);
dotlabel.rt("z2",z2);
draw z1{down}..{dir 45}z2;
endfig;The directions are given along the travel direction of the path, so a curve entering a point by going down looks the same as one leaving by going up etc.
The transform reflectedabout (p,q) can be used to mirror paths about the straight line from pair p to pair q.
Using this information along with what we have learned so far, try to draw an image like this:
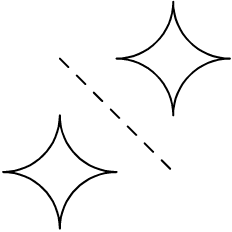
Hint
outputformat := "png";
outputtemplate := "%j_%c.png";
hppp := 0.25;
vppp := 0.25;
u:=0.5cm;
beginfig(1);
z0=-z1=(0,1u);
z2=-z3=(1u,0);
z4=(0,2u);
z5=(2u,0);
path p,m;
p:= z0{down}..{right}z2{left}..{down}z1{up}..{left}z3{right}..{up}z0;
m:= z4--z5;
draw p;
draw m dashed evenly;
draw p reflectedabout(z4,z5);
endfig;