For loops
For loops are great for handling repetitive elements in figures. MetaPost supports simple for loops over integers like this:
for i:=0 upto 10:
dotlabel("",(i,0));
endfor

dot dot dot
the upto form is shorthand for the full for loop syntax:
for i:0 step 1 until 10:
This full version allows us to change the step size, but most of the time step size 1 is fine so upto comes in handy.
For loops are also great for drawing functions, essentially by sampling our function at each step.
As a start, lets call the uniformdeviate function for some uniformly distributed noise:

step dependent noise.
for i:=0 upto 10:
dotlabel("",(i,uniformdeviate(i*2)));
endfor;But for a function we really want a smooth path through these points. Remember that paths start AND end with a pair. So we can do something like:
for i:=0 upto 10:
draw (i,uniformdeviate(i*2))..(i+1,uniformdeviate(i*2));
endfor;Essentially drawing each segment of the function. However the random noise makes the segments become disjointed.

Segmented paths.
Fortunately MetaPost has a solution to this problem, for-loops can be embedded into path definitions. So we can draw the image like this:
draw ( (0,uniformdeviate(0))
for i:=1 upto 10:
-- (i*u,uniformdeviate(u*i*2)) endfor);

One path.
Exercises
Another way of dealing with the segmented paths when drawing functions with randomness is to cache the results before drawing them. Try using two for loops, one to write function values in an array and another to draw line segments based on the array.
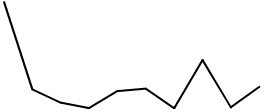
One path using two loops.
For some normal distributed noise you can use normaldeviate which does not take any parameters (standard normal distribution).
Hint
beginfig(5);
numeric gauss[];
for i:=1 upto 10:
gauss[i] := normaldeviate;
endfor;
for i:=1 upto 9:
draw (i*u,gauss[i]*u)..((i+1)*u,gauss[i+1]*u);
endfor;
endfig;